[Leetcode] Problem 963 - Minimum Area Rectangle II

Posted on | In ,

Given a set of points in the xy-plane, determine the minimum area of any rectangle formed from these points, with sides not necessarily parallel to the x and y axes.

If there isn’t any rectangle, return 0.

Example

No.1

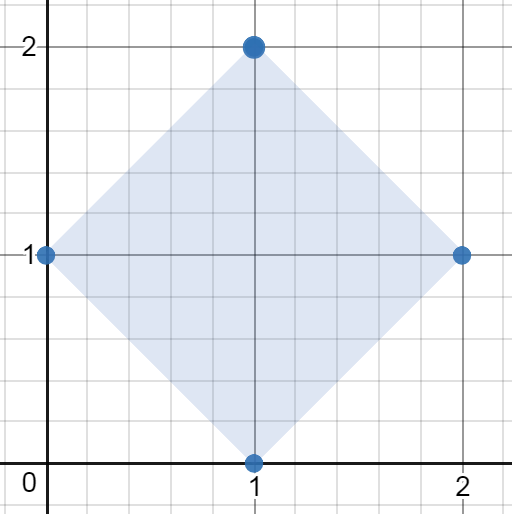
atUZW9.png

Input: [[1,2],[2,1],[1,0],[0,1]]

Output: 2.00000

Explanation: The minimum area rectangle occurs at [1,2],[2,1],[1,0],[0,1], with an area of 2.

No.2

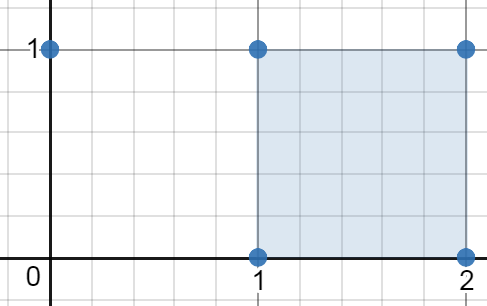
atUKL6.png

Input: [[0,1],[2,1],[1,1],[1,0],[2,0]]

Output: 1.00000

Explanation: The minimum area rectangle occurs at [1,0],[1,1],[2,1],[2,0], with an area of 1.

No.3

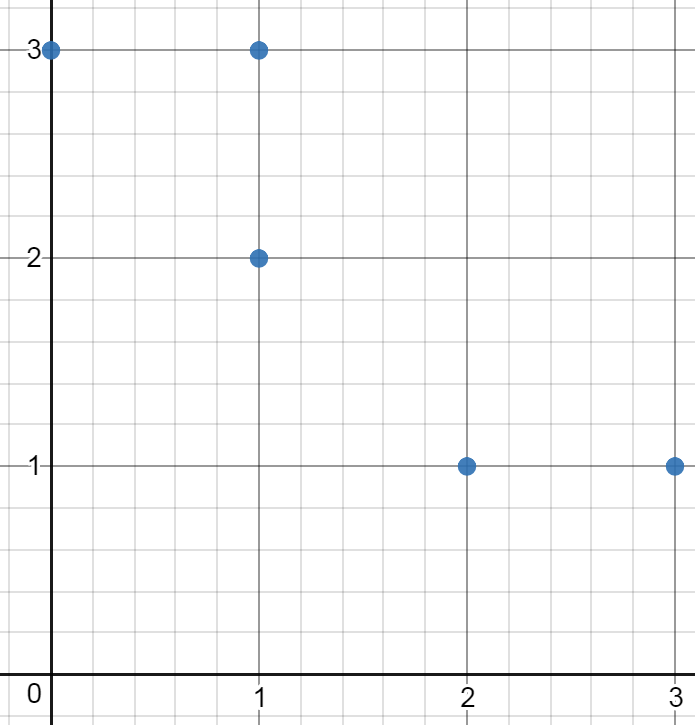
atUwef.png

Input: [[0,3],[1,2],[3,1],[1,3],[2,1]]

Output: 0

Explanation: There is no possible rectangle to form from these points.

No.4

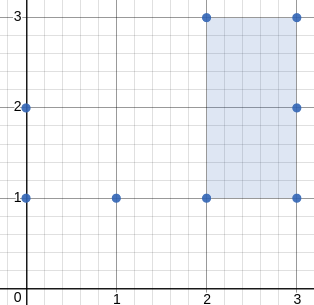
atUyWj.png

Input: [[3,1],[1,1],[0,1],[2,1],[3,3],[3,2],[0,2],[2,3]]

Output: 2.00000

Explanation: The minimum area rectangle occurs at [2,1],[2,3],[3,3],[3,1], with an area of 2.

Note

  1. 1 <= points.length <= 50
  2. 0 <= points[i][0] <= 40000
  3. 0 <= points[i][1] <= 40000
  4. All points are distinct.
  5. Answers within 10^-5 of the actual value will be accepted as correct.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public double minAreaFreeRect(int[][] points) {
    double result = Double.MAX_VALUE;

    Set<Integer> set = new HashSet<>();
    for (int[] point : points) {
        set.add(point[0] << 16 | point[1]);
    }

    int size = set.size();
    for (int i = 0; i < size; i++) {
        for (int j = 0; j < size; j++) {
            if (i == j)
                continue;
            
            for (int k = 0; k < size; k++) {
                if (k == i || k == j)
                    continue;

                int[] p0 = points[i];
                int[] p1 = points[j];
                int[] p2 = points[k];
                int dot = (p1[0] - p0[0]) * (p2[0] - p0[0]) + (p1[1] - p0[1]) * (p2[1] - p0[1]);
                if (dot != 0)
                    continue;

                int x3 = p1[0] + p2[0] - p0[0];
                int y3 = p1[1] + p2[1] - p0[1];
                if (!set.contains(x3 << 16 | y3))
                    continue;

                double a = Math.pow(p1[0] - p0[0], 2) + Math.pow(p1[1] - p0[1], 2);
                double b = Math.pow(p2[0] - p0[0], 2) + Math.pow(p2[1] - p0[1], 2);
                result = Math.min(a * b, result);
            }
        }
    }

    return result == Double.MAX_VALUE ? 0 : Math.sqrt(result);
}