[Leetcode] Problem 882 - Reachable Nodes In Subdivided Graph

Posted on | In ,

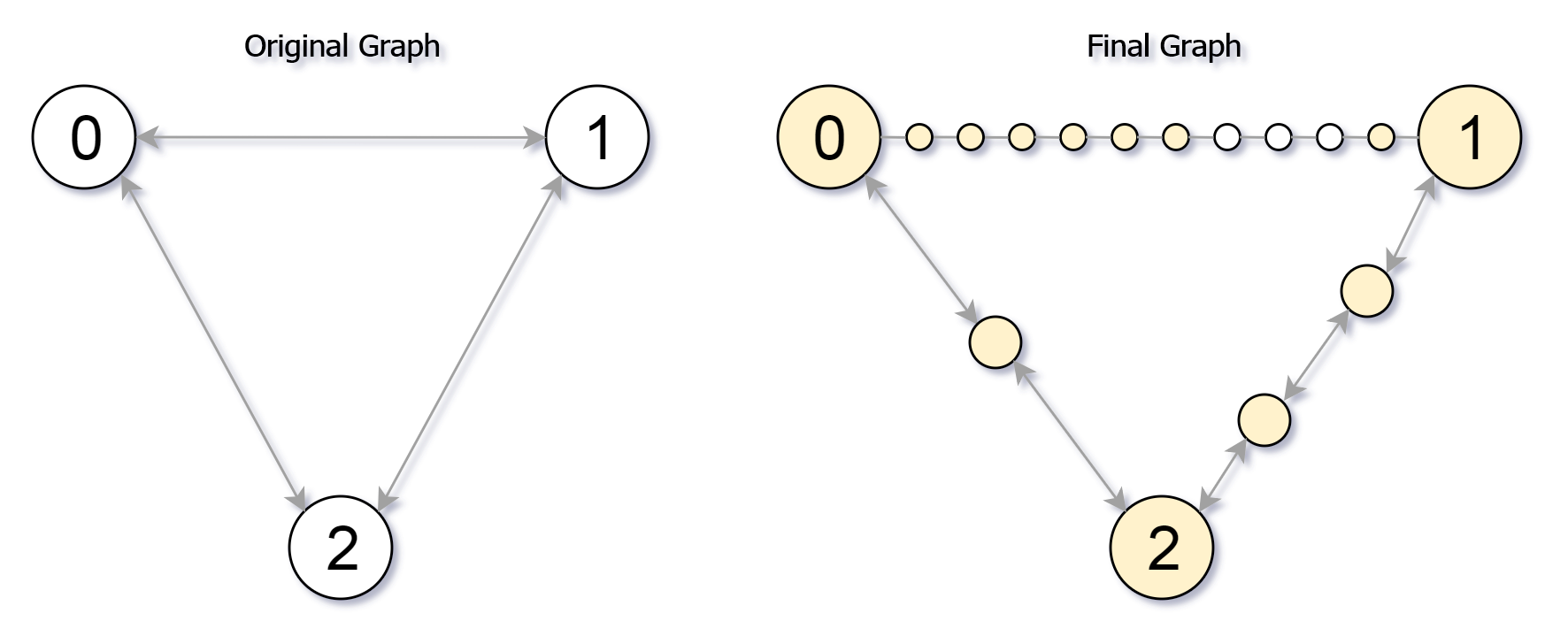
Starting with an undirected graph (the “original graph”) with nodes from 0 to N-1, subdivisions are made to some of the edges.

The graph is given as follows: edges[k] is a list of integer pairs (i, j, n) such that (i, j) is an edge of the original graph,

and n is the total number of new nodes on that edge.

Then, the edge (i, j) is deleted from the original graph, n new nodes (x_1, x_2, …, x_n) are added to the original graph,

and n+1 new edges (i, x_1), (x_1, x_2), (x_2, x_3), …, (x_{n-1}, x_n), (x_n, j) are added to the original graph.

Now, you start at node 0 from the original graph, and in each move, you travel along one edge.

Return how many nodes you can reach in at most M moves.

Example

No.1

Input: edges = [[0,1,10],[0,2,1],[1,2,2]], M = 6, N = 3

Output: 13

Explanation:
The nodes that are reachable in the final graph after M = 6 moves are indicated below.

w2rjIJ.png

No.2

Input: edges = [[0,1,4],[1,2,6],[0,2,8],[1,3,1]], M = 10, N = 4

Output: 23

Note

  1. 0 <= edges.length <= 10000
  2. 0 <= edges[i][0] < edges[i][1] < N
  3. There does not exist any i != j for which edges[i][0] == edges[j][0] and edges[i][1] == edges[j][1].
  4. The original graph has no parallel edges.
  5. 0 <= edges[i][2] <= 10000
  6. 0 <= M <= 10^9
  7. 1 <= N <= 3000
  8. A reachable node is a node that can be travelled to using at most M moves starting from node 0.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
public class Node{
    private int idx;
    private int val;

    public Node(int idx, int val) {
        this.idx = idx;
        this.val = val; 
    }
}

public int reachableNodes(int[][] edges, int M, int N) {
    List<Node>[] graph = new ArrayList[N];
    Map<Integer, Integer> visit = new HashMap<>();
    PriorityQueue<Node> pq = new PriorityQueue<>((a, b) -> (b.val - a.val));
    pq.offer(new Node(0, M));
    
    for (int i = 0; i < N; i++)
        graph[i] = new ArrayList<Node>();

    for (int[] edge : edges) {
        graph[edge[0]].add(new Node(edge[1], edge[2] + 1));
        graph[edge[1]].add(new Node(edge[0], edge[2] + 1));
    }

    while (!pq.isEmpty()) {
        Node node = pq.poll();

        if (!visit.containsKey(node.idx)) {
            visit.put(node.idx, node.val);

            for (Node neighbor : graph[node.idx]) {
                int val = node.val - neighbor.val;

                if (visit.containsKey(neighbor.idx) || val < 0)
                    continue;

                pq.offer(new Node(neighbor.idx, val));
            }
        }
    }

    int result = visit.size();

    for (int[] edge : edges) {
        int a = visit.containsKey(edge[0]) ? visit.get(edge[0]) : 0;
        int b = visit.containsKey(edge[1]) ? visit.get(edge[1]) : 0;
        result += Math.min(edge[2], a + b);
    }

    return result;
}