[Leetcode] Problem 1373 - Maximum Sum BST in Binary Tree

Posted on | In ,

Given a binary tree root, the task is to return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).

Assume a BST is defined as follows:

  • The left subtree of a node contains only nodes with keys less than the node’s key.
  • The right subtree of a node contains only nodes with keys greater than the node’s key.
  • Both the left and right subtrees must also be binary search trees.

Example

No.1

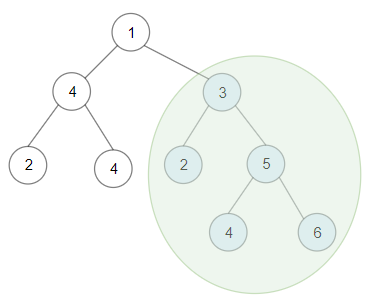
0yIRx0.png

Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]

Output: 20

Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.

No.2

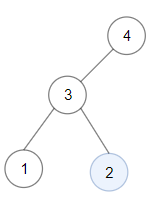
0yIvqO.png

Input: root = [4,3,null,1,2]

Output: 2

Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.

No.3

Input: root = [-4,-2,-5]

Output: 0

Explanation: All values are negatives. Return an empty BST.

No.4

Input: root = [2,1,3]

Output: 6

No.5

Input: root = [5,4,8,3,null,6,3]

Output: 7

Constraints

  • The given binary tree will have between 1 and 40000 nodes.
  • Each node’s value is between [-4 * 10^4 , 4 * 10^4]

Code

1
2
3
4
5
6
7
8
9
10
11
12
public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public class Node {
    private int min;
    private int max;
    private boolean isBST;
    private int sum;

    public Node(int min, int max, boolean isBST, int sum) {
        this.min = min;
        this.max = max;
        this.isBST = isBST;
        this.sum = sum;
    }
}

private int result = 0;

public int maxSumBST(TreeNode root) {
    dfs(root);
    return result;
}

private Node dfs(TreeNode root) {
    if (root == null)
        return new Node(Integer.MAX_VALUE, Integer.MIN_VALUE, true, 0);

    Node left = dfs(root.left);
    Node right = dfs(root.right);

    boolean isBST = left.isBST && right.isBST && root.val > left.max && root.val < right.min;
    int sum = isBST ? left.sum + right.sum + root.val : -1;
    result = Math.max(result, sum);
    return new Node(Math.min(left.min, root.val), Math.max(right.max, root.val), isBST, sum);
}