[Leetcode] Problem 1483 - Kth Ancestor of a Tree Node

Posted on | In ,

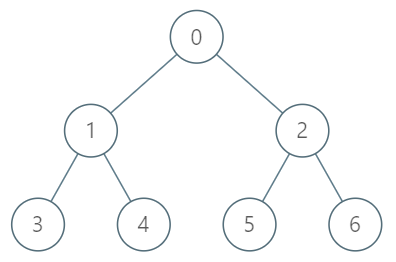
You are given a tree with n nodes numbered from 0 to n-1 in the form of a parent array where parent[i] is the parent of node i. The root of the tree is node 0.

Implement the function getKthAncestor(int node, int k) to return the k-th ancestor of the given node. If there is no such ancestor, return -1.

The k-th ancestor of a tree node is the k-th node in the path from that node to the root.

Example

0yOP76.png

Input:
[“TreeAncestor”,”getKthAncestor”,”getKthAncestor”,”getKthAncestor”]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]

Output:
[null,1,0,-1]

Explanation:

1
2
3
4
5
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);

treeAncestor.getKthAncestor(3, 1);  // returns 1 which is the parent of 3
treeAncestor.getKthAncestor(5, 2);  // returns 0 which is the grandparent of 5
treeAncestor.getKthAncestor(6, 3);  // returns -1 because there is no such ancestor

Constraints

  • 1 <= k <= n <= 5*10^4
  • parent[0] == -1 indicating that 0 is the root node.
  • 0 <= parent[i] < n for all 0 < i < n
  • 0 <= node < n
  • There will be at most 5*10^4 queries.

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// A(x, k) = A(A(x, t), k - t), 1 <= t < k
// A(x, 0) = x
// A(0, >0) = -1
// dp[i][j]: node j's 2^i-th ancestor
// dp[i][j] = dp[i - 1][dp[i - 1][j]] // A(j, 2^i) = A(A(j, 2^(i-1)), 2^(i-1))

private int count;
private int[][] dp;

public TreeAncestor(int n, int[] parent) {
    count = (int) Math.ceil(Math.log(n) / Math.log(2));
    dp = new int [count][n];
    dp[0] = parent;

    for (int i = 1; i < count; i++) {
        for (int j = 0; j < n; j++) {
            int prev = dp[i - 1][j];
            dp[i][j] = prev == -1 ? -1 : dp[i - 1][prev];
        }
    }
}

public int getKthAncestor(int node, int k) {
    if (k == 0)
        return node;

    for (int i = count - 1; i >= 0 && node != -1; i--) {
        if ((k & (1 << i)) != 0) {
            node = dp[i][node];
        }
    }

    return node;
}